1. La loi normale centrée réduite

Si nous substituons à la variable x, la variable normée u nous obtenons la loi normale centrée réduite.
Sa moyenne est égale à 0. L'unité de la variable est .
On peut ainsi calculer la valeur de u correspondant à toute valeur de x.

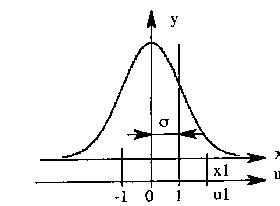(fig1)

Exemple : pour une loi normale de moyenne m=10,25mm et d'écart-type = 0,135 mm, la valeur u1 correspondant à x1=10,52 mm est : fig 1.

2. La fonction de répartition de la loi normale centrée réduite

La transformation d'une loi normale qelconque en loi normale centrée réduite nous permet de connaître les probabilités associées à la loi normale.
Ces probabilités sot fournies par la table de la loi normale cetrée réduite (voir tables 1-2 et 1-3).

• Utilisation de la table 1-2

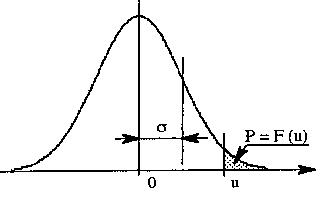
  Pour une valuer de u donnée, on lit P=F(u) dans le corps de la table (aire hachurée sur la fig2)
  Les interpétations en sont les suivantes :

  • dans une population normale, la totalité des individus est conventionnellement égale à 1, la proportion de ceux-ci se situant en dessous de u est égale à F(u)=P
  • si l'on prélève, au hazard, un individu dans une population normale, la probabilité P pour qu'il ait une valuer inférieure à x = u.+ m est donnée par la table.

  Par exemple :

  • si u=2, P=F(u)=0,9772
  • si u=-2, P=1-F(u)=1-0,9772=0,0228

   

• Utilisation de la table 1-3

  Pour une valeur de P donnée, on lit u dans le corps de la table.
  Les interprétations en sont les suivantes :

  • dans une population normale, la totalité des individus est conventionnellement égale à 1, la proportion de ceux-ci se situant en dessus de u est égale à F(u)=P
  • si l'on prélève, au hazard, un individu dans une population normale, la probabilité P pour qu'il ait une valuer inférieure à x = u.+ m est donnée par la table.

  Par exemple :

  si P=0,15	u=1,0364
  si P=0,204	u=0,8274
  si P=0,001 (1 pour mille)	u=3,09...
  si P=0,025 (2,5%)	u=1,96...
  si P=0,999 (999 pour mille)	u=-3,09...
  si P=0,975 (97,5%)	u=-1,96

  (fig2)

  Remarque : on obtient généralement les valeurs caractéristiques
  u = 1,96 pour P = 97,5% soit 1-P=2,5%
  u = 3,09 pour P = 99,9% soit 1-P=0,1%

	99,8% de la population		99,8% de la population
(fig3)		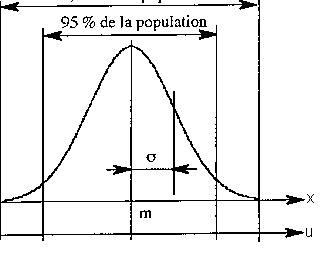(fig4)
........-3,09...... -1,96 ......................0........................1,96........3,09...............		.........-3...........-2...........................0............................2...........3............

3. Application

On dispose d'un lot de flacons dont la moyenne de la hauteur est m = 52,42mm et l'écart-type est de = 0,152mm.
Les limites de tolérances sont Ts = 52,7mm et Ti = 52,3 mm.
Déterminer le pourcentage de rebut correspondant.
On calcule les valeurs de u (loi normale centrée réduite) correspondant à Ts et à Ti et on évalue le rebut corresondant.

	(arrondi à 0,79) d'où P = 0,7852 (lu dans la table)
et P1 = 1 - 0,7852 = 0,2148	(arrondi à 0,215)
	(arrondi à 1,84) d'où P = 0,9671 (lu dans la table)
et P2 = 1 - 0,9671 = 0,033

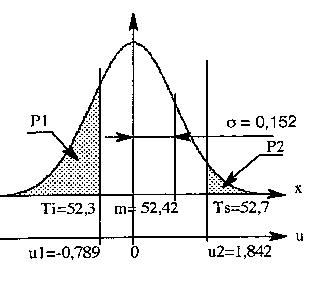(fig 5)

Le rebut total est de P1 + P2 = 0,215 + 0,033 = 0,248 soit environ 25 %

4. Construction pratique d'une courbe de Gauss

On peut construire simplement une courbe de Gauss à partir de quelques points. Le coefficient indiqué est à multiplier par la valeur de son choix pour obtenir une courbe plus ou moins aplatie.

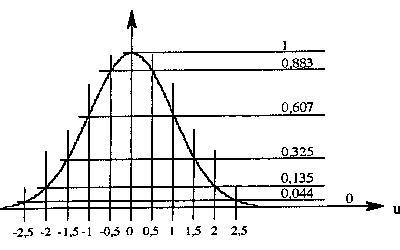(fig 6)	Exemple d'application : pour obtenir une couorbe de hauteur 38 mm
	u	constante	ordonnée
	-2,5 ou 2,5 -2 ou 2 -1,5 ou 1,5 -1 ou 1 -0,5 ou 0,5 0	0,044 0,135 0,325 0,607 0,883 1	1,7 5,1 12,3 23,1 33,6 38

Remarquez la forme arrondie du sommet.