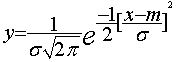| Tous les phénomènes
naturels obéissent à des lois de probabilité plus
ou moins complexes. Très souvent, on peut pourtant, sous certaines
conditions, en faire l'approximation par des lois normales
1. Les lois normales
Lorsqu'une grandeur subit l'influence de nombreuses causes indépendantes
et dont aucune d'entre elles n'est prépondérante, elle
obéit généralement à une loi normale.
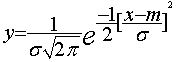 |
Y exprime la densité de probabilité
de x |
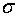
m
e
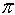 |
= écart type
= moyenne
= 2.71828
=3.14159 |
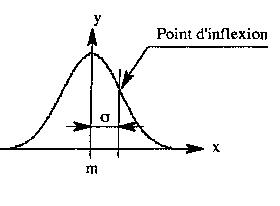 |
La courbe représentative de ces probabilités
a la forme d'une cloche d'où le nom de "courbe en
cloche" souvent atribué à ces populations.
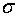 situe le point d'inflexion
de la courbe par rapport à la moyenne m. situe le point d'inflexion
de la courbe par rapport à la moyenne m.
|
2. Calcul des paramètres
d'une loi normale
Si l'on dispose de tous les individus d'une population (ou
d'un échantillon suffisamment représentatif) :
on peut calculer les paramètres de la loi normale correspondante.
- La moyenne m (caractérise la position)
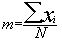 , avec Xi
= individus et N = nombre d'individus (effectif) , avec Xi
= individus et N = nombre d'individus (effectif)
- L'écart type
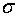 (caractérise
la dispersion) (caractérise
la dispersion)
L'expression correspondant au calcul de la moyenne est
connue de tous. par contre, pour l'écart type, il
faut :
- calculer l'écart qui sépare chaque individu
de la moyenne,
- élever au carré ces écarts (ce qui
a, en particulier, pour effet de rendre toutes les valeurs
positives),
- calculer la moyenne de la somme de tous ces écarts
élevés au carré,
- ce résultat s'appelle la variance.
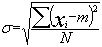
Nota : cet écart-type correspond
à l'écart-type d'une population dont on a pris
en compte tous les individus. Il ne faut surtout pas le confondre
avec s qui est une estimation de 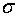 . .
La moyenne caractérise la position de la distribution.
On dira, par exemple, que le diamètre de tournage est
de 27,6 mm. C'est aussi le centre de gravité des valeurs.
L'écart-type caractérise la dispersion des valeurs
de part et d'autre de cette moyenne. Plus l'écart-type
est grand et plus la dispersion est grande également.
Il est indispensable de connaître la loi de distribution
pour porter un jugement satisfaisant sur la population.
- Le coefficient de variation (CV % caractérise
la dispersion relative)
|
|