L'analyse de la variance - Test de Fisher -
Test sur l'existence d'une pente significative
Test d'influence
La
seule analyse d'une régression par son coefficient de corrélation
et par le coefficient directeur de
la droite n'est pas suffisant pour tester l'influence de x sur y.
Le
test de Fischer fournit une estimation de cette influence. Il est
surtout ut-lie en régression multiple
où l'on peut analyser plusieurs facteurs à la fois. Dans
ce cas les calculs sont longs et fastidieux. Des logiciels d'analyse
de la variance permettent de
s'en affranchir. Le
but de ce chapitre est d'expliquer le principe du test qui est transposable
en régression multiple.
1
- Les variances
2 - Analyse
de la variance
Sur
une régression, on peut calculer trois variances distinctes :
-
la
variance totale . C'est la variance classique. 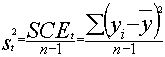
Cette
variance est égale à l'écart-type s au carré de
toutes les valeurs de y.
SCE t représente la somme des carrés des écarts totaux
sur y.
Exemple avec les valeurs du tableau ( graphique )
| n° | dimension n°1 | dimension n°2 | Les valeurs de chaque ligne appartiennent au même individu. On a relevé deux dimensions et le numéro d'ordre de production. |
| 1 | 30 | 9 | |
| 2 | 40 | 24 | |
| 3 | 21 | 8 | |
| 4 | 38 | 14 | |
| 5 | 27 | 0 | |
| 6 | 23 | 0 | |
| 7 | 30 | 4 | |
| 8 | 29 | 13 | |
| 9 | 43 | 19 | |
| 10 | 35 | 10 |
La variance est calculée à partir des segments correspondants représentés en traits forts sur la figure.
-
la
variance résiduelle ( graphique
)
-
SCE
représente la somme des carrés des écarts résiduels.
On
peut aussi l'estimer à partir des résultats fournis par
une calculatrice permettant les calculs de régression
(pour des lois normales) :
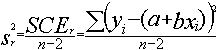 |
|
Cette variance résiduelle est la variance due aux facteurs autres que le (ou les) facteur(s) pris en compte. La variance est calculée à partir des segments correspondants représentés en traits forts sur le graphique.
-
la
variance due au facteur _________________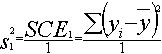
Elle correspond à la variance due à la pente de la droite c'est à dire au facteur pris en compte dans la régression (x).
- SCE1 représente la somme des carrés des écarts provoqués par la régression linéaire.
On
peut calculer SCE1 par la formule suivante: SCE1
= b![]()
![]() (x1-
(x1-![]() )
)
(b est le coefficient
directeur de la droite de régression linéaire)
La variance est calculée à partir des segments correspondants représentés en traits forts sur le graphique .
Les résultats correspondant à l'analyse de la variance sont regroupés dans un tableau dit d'analyse de la variance.
| Origine de la variation | Somme des carrés des écarts | Dégré de liberté (DDL) | Carré moyens (variances) | Ftest |
| Régression linéaire erreur (résiduelle) |
SCE1 SCEr |
1 n - 2 |
s s |
(SCE1/1) / (SCEr/n-2) |
| Total | SCEt |
n - 1 |
s |
n = nombre total d'observations,
F test = variable de Fisher pour le test,
Pour faciliter les calculs, on note que: SCEt = SCE + SCEr
Pour les valeurs de l'exemple:
L'hypothèse Ho est: la pente de la droite est significativement différente de 0.
sy=7,7667
d'où SCEt=
7,7667![]() x 9 =542,9
x 9 =542,9
sX=
7,2449 d'où
s![]() x =
52,489
x =
52,489
Coefficient
directeur b = 0,85182 ![]() (x1
-
(x1
- ![]()
![]() )
= s
)
= s![]() x(n-1)
= 52,489 x 9 = 472,4
x(n-1)
= 52,489 x 9 = 472,4
d'où SCE1 = 0,8518 x 0,8518 x 472,4 = 342,8
et SCEr = 542,9 - 342,8 = 200,1
| Origine de la variation | Somme des carrés des écarts | Dégré de liberté (DDL) | Carré moyens (variances) | Ftest |
| Régression linéaire erreur (résiduelle) |
342,8 200,1 |
1 8 |
342,8 25,0 |
342,8/25,1 =13,7 |
| Total | 542,9 |
9 |
Si
Ftest
dépasse
la valeur fournie par la table (extrait du tableau ci-dessous),
la pente de la droite est significative et
l'on considère que l'effet du facteur x
est significatif (risque ![]() = 5 %)
= 5 %)
Extrait
de la table du F
pour un risque
![]() de 5 %
(dans ce cas:
de 5 %
(dans ce cas: ![]() 1
= 1 et
1
= 1 et ![]() 2
=
n - 2)
2
=
n - 2)
| Extrait
de la table du F pour |
Ftable | |
1 |
161 |
|
| 2 |
18,5 |
|
3 |
10,1 |
|
| 4 |
7,71 |
|
5 |
6,61 |
|
| 6 |
5,99 |
|
7 |
5,59 |
|
| 8 |
5,32 |
|
9 |
5,12 |
|
| 10 |
4,96 |
|
11 |
4,84 |
F(0,95;1;9) = 5,32
L'influence de x est donc significative au risque de 5 % puisque 13,7 est plus grand que les 5,32 prévus par la table.
L'hypothèse
Ho est acceptée. La pente de la droite de
régression est significativement différente de
0(![]() =0,05)
=0,05)