Test de Dixon
Le test de Dixon est un test numérique dont l'objet est de détecter les valeurs aberrantes contenues dans un ou des échantillons en vue de leur élimination.
Ce type de test peut rendre service lorsqu'on ne connait pas "l'histoire" des valeurs. Dans de nombreux cas, on peut éviter d'y faire appel dans un but de simplification évidente. La connaissance de l'origine des valeurs et de la méthode de prise d'échantillons est souvent suffisante sur un site de production.
1. Application à un échantillon unique (USP XVI)
2. Application à plusieurs échantillons
3. Tableau : valeurs critiques (extrait de ISO 5725 - NFX 06 041)
1. Application à un échantillon unique (USP XVI)
- Mode opératoire
- classer les valeurs dans l'ordre croissant,
- calculer l'étendue R de l'échantillon : R = xn-x1
- calculer la différence entre chacune des 2 valeurs voisines situées aux extrémités de la série : xn-x(n-1) et x2 - x1
- on retient la plus grande de ces 2 différences qui correspond à la valeur extrême la plus critique.
- calculer le quotient différence la plus forte / R = Qt
- si ce quotient Qt est plus élevé que la valeur
correspondante de la table,
on considère que la valeur testée est aberrante
(risque
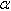=0,05)
- Exemple d'application
Soit l'échantillon :
9,95 |
9,99 |
9,99 |
10,01 |
10,03 |
10,03 |
10,03 |
10,04 |
10,05 |
10,07 |
R = 10,07 - 9,95 = 0,12 x10 - x9 = 10,07 - 10,05 = 0,02 x2 - x1 = 9,99 - 9,95 = 0,04 Qt = 0,04/0,12 = 0,33 Qt = 0,33 est inférieur ) la valeur de la table 1 pour n = 10 : Q10,0,95 = 0,41 Conclusion : on concidère que la valeur de la table 9,95 n'est pas aberrante (
2. Application à plusieurs échantillons
- Mode opératoire
- classer les valeurs de chaque échantillon dans l'ordre croissant,
- calculer l'étendue R de chaque échantillon : Ri
- effectuer la somme de ces étendues :
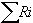
- identifier l'étendue maximale des échantillons : Rmax
- calculer le Q't = Rmax /
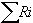
- si ce quotient Q't est plus élevé que la valeur
correspondante de la table,
on considère que la valeur testée est aberrante
(risque 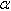=0,05)
- Exemple d'application
Soit l'échantillon :
| k |
valeurs |
R |
|||||
| 1 |
37,21 |
37,77 |
39,84 |
44,57 |
45,87 |
47,25 |
10,04 |
| 2 |
35,40 |
40,04 |
42,25 |
45,35 |
49,05 |
50,07 |
14,67 |
| 3 |
32,5 |
41,08 |
41,67 |
43,26 |
44,73 |
46,13 |
13,63 |
| somme des R=38,34 |
|||||||
Qt = 14,67 / 38,34 = 0,38
Valeur de Q' dans la table 2 pour n = 6 et k = 3 : 0,39
Conclusion : on considère qu'aucune valeur des échantillons n'est abérrante (
