La comparaison des variance d'échantillons permet de dire si les variances de deux populations sont égales ou non avec un risque choisi.

1 - Domaine d'application
2- Caractéristiques nécessaires au test
3 - Mode opératoire
4 - Application du test
5 - Compléments concernant l'utilisation de la table de Fisher Snedecor

1 - Domaine d'application

Les populations sont supposées normales sauf si l'effectif de chaque échantillon est important (n>30). Un test de normalité peut être pratiqué si nécessaire.

2- Caractéristiques nécessaires au test

Deux populations sont à prélever au hasard dans chacune des deux populations qui peuvents être constituées par des résultats d'essais.
Il est toujours nécessaire d'identifier les sources de prélèvements afin d'en assurer l'identification.

Chacun des deux échantillons est caractérisé par :

• les valeurs individuelles ( xi ),
• le nombre de valeurs n,
• l'écart-type des valeurs (s).

La comparaison des deux variances reviens à tester le quotient des deux variances par rapport à 1.

On vérifie que ce quotient est situé dans un intervalle de confiance déterminé par les limites extraites de la table du F de Fisher Snedecor pour un risque choisi.

Dans la pratique, on calcule le quotient de la variance la plus élevée sur la variance la plus faible ce qui permet d'utiliser directement la valeur du F correspondant à la borne supérieure de l'intervalle de confiance.

3 - Mode opératoire

Calcul de la variance de chacun des échantillons
Détermination du nombre de degré de liberté pour chacun des échantilons.	= n - 1

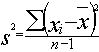• Détermination de la valeur du F limite de la table
• On choisit la table du F correspondant à un risque 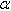choisi. si 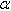=5%, on prend la table à 0,95.
• Conclusion du test

4 - Application du test

On se propose de tester l'égalité des variances concernant deux procédés de production pour lesuels on a obtenu les résultats du tableau ci-dessous. les populations obéissent à des lois normales.

Ce test précède un test d'égalité de deux moyennes afin de comparer les deux procédés.

	Procédé 1	Procédé 2
valeurs	8,32	15,84
	8,60	15,10
	9,02	15,99
	8,70	14,26
	10,43	14,02
	10,53	14,62
	9,84	15,95
	12,54	14,79
	11,56	14,28
	9,06	14,45
	-	15,72
	-	14,80
n	10	12
	9	1
variance	1,9411	0,5155

On calcule le quotient de la plus grande des deux variances sur la plus petite :

• F test = 1,9411 / 0,5155 = 3,77
• F table = F 0,95;9;11 = 2,90
• F test > F table

Conclusion : les variances sont significativement différentes l'une de l'autre ( risque = 5% ).

Conséquence : on ne peut valablement pas effectuer le test de comparaison des moyennes.

Dans ce cas, il y a lieu de chercher la cause de cette différence avant de poursuivre les tests sur les moyennes.

5 - Compléments concernant l'utilisation de la table de Fisher Snedecor

Comparaison de deux variances :

Pour comparer deux variances, on utilise :

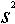• k = variance de chaque échantillon
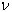• k = nombre de degrés de libertés de chaque échantillon

La comparaison se fait à l'aide du quotient de la variance la plus forte sur la variance la plus faible. Exemple : en supposant que la variance de l'échantillon A est plus élevé que celle de B.

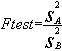		La comparaison de Ftest et de Ftable permet de conclure
F table = F(1-/2 ; A ; B)