Les histogrammes
Un histogramme est une repésentation graphique des effectifs d'une population classée par intervalles. Sur l'axe des abscisses, on porte les caractéristiques de l'intervalle (ou classe) et sur l'axe des ordonnées le nombre d'individus dans chaque intervalle.
- Domaine d'emploi
- Mise en oeuvre
- Exemple de construction d'un histogramme
- Exemple d'analyse d'histogramme
- Fiche d'essai : étude de la normalité d'un échantillon (droite de Henry)
L'histogramme est essentiellement pour visualiser certains phénomènes. Leur analyse permet la mise en évidence de l'allure de la distribution et permet parfois de détecter certaines anomalies.
La comparaison d'un histogramme à un modèle connu permet simplement de raccorder la distribution à la loi référence.
Il faut distinguer deux types d'histogrammes :
- Les histogrammes pour les variables continues
Chaque classe est représentée par un rectangle dont la base d'identifie à l'amplitude de la classe et dont la hauteur est proportionnelle à l'effectif.
Par convention et dans chaque classe, la borne inférieure est inclue et la borne supérieure exclue (c'est à dire que si une valeur est égale à la valeur d'une borne, elle sera affectée à la classe inférieure).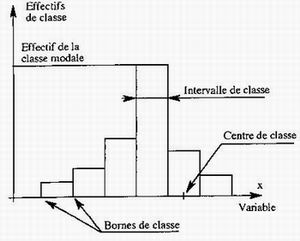
Remarque : Le choix du nombre de classes est déterminant. S'il est trop grand ou trop petit, on risque de perdre une grande partie de l'information que l'histogramme peut contenir.
Certains préconisent un nombre de classes égal à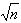 (n étant
l'effectif total) mais ceci ne doit pas constituer une régle
absolue. Une douzaine de classes donne très souvent satisfaction
mais on peut toujours construire plusieurs histogrammes différents
(exemple : un histogramme dont les classes correspondent aux
nombres pairs et impairs peut permettre de mettre en évidence
l'usage d'un appareil de mesure ne prenant en compte que les
valeurs paires, par exemple l'usage d'un pied à coulisse
au 1/50ième de mm).
(n étant
l'effectif total) mais ceci ne doit pas constituer une régle
absolue. Une douzaine de classes donne très souvent satisfaction
mais on peut toujours construire plusieurs histogrammes différents
(exemple : un histogramme dont les classes correspondent aux
nombres pairs et impairs peut permettre de mettre en évidence
l'usage d'un appareil de mesure ne prenant en compte que les
valeurs paires, par exemple l'usage d'un pied à coulisse
au 1/50ième de mm).
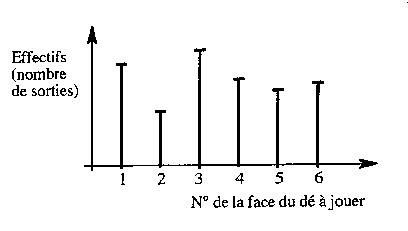
Le représentation est effectuée sous la forme de "bâtons".
Par exemple, pour une série de jets de dés, les probabilités de sorties de chacun des numéros sont égales, chacun des effectifs de sortie doit tendre vers le nombre de sorties divisé par 6.
Des inégalités trop importantes peuvent permettre de détecter un truquage ou un défaut du dé.
3. Exemple de construction d'un histogramme
Soit la liste de 60 valeurs obtenues à la suite d'un relevé métrologique :
| 58 | 57 | 55 | 42 | 50 | 50 | 51 | 58 | 59 | 62 | 61 | 63 | 60 | 55 | 58 |
| 54 | 56 | 54 | 53 | 56 | 57 | 54 | 59 | 56 | 55 | 59 | 58 | 58 | 58 | 50 |
| 60 | 59 | 58 | 57 | 59 | 56 | 57 | 39 | 65 | 53 | 48 | 41 | 55 | 58 | 57 |
| 59 | 57 | 58 | 54 | 58 | 60 | 58 | 59 | 59 | 52 | 58 | 59 | 60 | 60 | 57 |
Tableau d'analyse
Nombre de classe |
limite de classes |
centres de classes |
effectifs de classes |
1 |
x<40 |
38,5 |
1 |
2 |
40<=x<43 |
41,5 |
2 |
3 |
43<=x<46 |
44,5 |
0 |
4 |
46<=x<49 |
47,5 |
1 |
5 |
49<=x<52 |
50,5 |
4 |
6 |
52<=x<55 |
53,5 |
7 |
7 |
55<=x<58 |
56,5 |
15 |
8 |
58<=x<61 |
59,5 |
26 |
9 |
61<=x<64 |
62,5 |
3 |
10 |
64<=x |
65,5 |
1 |
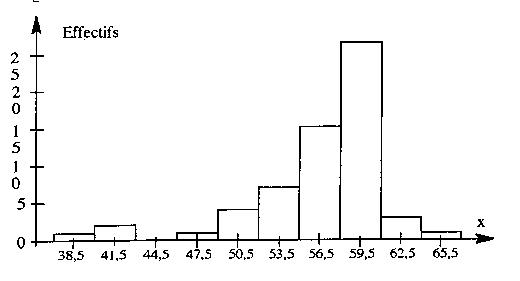 |
Observations : Cet histogramme lisse apparaître une certaine asymétrie. les trois valuers les plus faibles le sont sans doute anormalement. Cette population n'infirme pas l'hypothèse de normalité de la population. |
4. Exemple d'analyse d'histogramme
- Distribution tronquées (résultant d'un tri)
| Elimination des valeurs centrales | Elimination des valeurs latérales | Elimination des valeurs basses |
 |
||
| Distribution autour d'un axe centré sur la moyenne (distribution de Rayleigh) | Distribution autour d'un axe excentré par rapport à la référence de mesurage | |
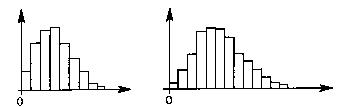 |
||
| Distribution symétrique
par rapport à l'origine de mesure (0) (loi demi normale) |
Distribution autour d'une référence décalée par rapport à l'origine de mesurage (0) | |
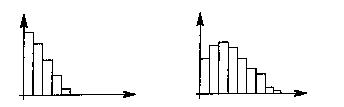 |
||
- Mélange de plusieurs populations normales
| Mélange de deux populations de moyennes voisines | Mélange de deux populations de moyennes assez éloignées | |
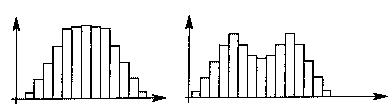 |
||
Observations :
L'examen d'un histogramme permet souvent de détecter des anomalies.
La plupart du temps, l'observation de la distribution doit s'accompagner d'une "enquête" sur les origines de la population. Les questions essentielles que l'on peut se poser sont :
- que représente les mesures ? (nature de la population)
- comment les mesures ont-elles été pratiquées ? (moyen de mesure, lecture des résultats, etc.)
- y a t'il eu possibilité de mélange de population ? (fabrication par plusieurs machines)
- y a t'il eu possibilité de tri des individus ?
Rappels :
- Une distribution normale résulte d'une population dont le caractére étudié est influencé par de nombreux facteurs dont aucun n'est prépondérant par rapport aux autres,
- Une loi normale varie, en théorie de moins l'infini à plus l'infini. attention aux distributions limitées aux valeurs positives et proche de zéro. (voir ci-dessus les coaxialité et symétrie)
- Une distribution normale est symétrique par rapport à sa moyenne