|
La loi de Student est une loi d'échantillonnage. Elle trouve
ses applications dans le domaine des tests sur la moyenne d'échantillons
de lois normales.
La loi de Student est due à W.S. Gosset dit "Student"
qui l'a mise au point à l'occasion de travaux pour le compte
des brasseries Guinness à Dublin au début du 20ième
siècle.
- Expression algébrique de la loi de
Student
- Lecture de la table de la loi de Student
- Distribution des moyennes d'échantillons
- Intervalle de confiance d'une moyenne
- Exemple d'application
- Construction d'un intervalle de confiance
de la moyenne
- Calculs pratiques
- Exemple
- Fiche
d'essai
- Expression algébrique de la loi de Student
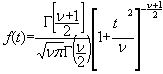 |
 = fonction
gamma = fonction
gamma- t = variable de Student
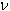 = nu = nombre
de degrés de liberté = nu = nombre
de degrés de liberté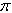 =3,14159 =3,14159 |
Graphique de la loi : cliquez
ici
Il existe une loi de Student par degré de liberté
d'où la complexité de la table. Dans le cas d'un test
de Student sur les moyennes le nombre de degrés de liberté
n est égal à n-1 car on utilise une moyenne estimée
dans les calculs.
- Lecture de la table de la loi de Student
A chaque ligne de la table correspond une loi de Student.
la table fournit les valeurs positives de t pour des fractiles choisis.
Les valeurs ngatives sont obtenues par symétrie.
- Distribution des moyennes d'échantillons
On montre, en effet, que les moyennes des échantillons
issus d'un loi normale de moyenne m et d'écart-type 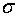 obeissent
à une loi de Studnt de moyenne m et d'écart-type obeissent
à une loi de Studnt de moyenne m et d'écart-type 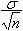 . .
Graphiques :
- distribution des valeurs de la population (N, M, 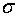 )
: cliquez
ici )
: cliquez
ici
- distribution des moyennes des échantillons de taille n
issus de la loi (N, M, 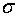 )
: cliquez
ici )
: cliquez
ici
En pratique, on ne connait pas les paramètres de
la loi de distribution de la population. On se propose alors de
l'estimer par l'intermédiaire d'un échantillon qui
peut être de taille réduite. Dans ce cas, on utilise
les propriétés de la loi de Student pour déterminer
un intervalle de confiance
de la moyenne vraie m.
Un risque 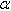 est choisi. Il est le plus souvent de 5%.
est choisi. Il est le plus souvent de 5%.
Nota : lorsque l'échantillon est de taille suffisante (n>30)
et que l'on connait l'écart-type de la population, on peut
utiliser une approximation de la loi de Student par une loi normale
plus simple d'emploi.
- Intervalle de confiance d'une moyenne
Graphique de la loi : cliquez
ici
- Exemple d'application
- Construction d'un intervalle de confiance de la moyenne
Afin d'estimer la moyenne d'une population, on construit un
intervalle de confiance autour de la valeur expérimentale
de la moyenne ( ). ).
La valeur de t est lue dans la table pour :
- un risque 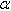 choisi. Pour un risque bilatéral de 5%, on lit la valeur
de t dans la colonne 0,975
choisi. Pour un risque bilatéral de 5%, on lit la valeur
de t dans la colonne 0,975
- un nombre de degrés de liberté 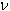 (nu) (DDL) égal à n-1 à cause de l'estimation
de la moyenne m par
(nu) (DDL) égal à n-1 à cause de l'estimation
de la moyenne m par  lors du calcul de l'écart-type s.
lors du calcul de l'écart-type s.
Graphique de la loi : cliquez
ici
- Calculs pratiques
On prélève un échantillon de taille
n par tirage aléatoire dans la population.
On calcul :
La valeur de t est choisie dans la table de Student. Elle permet
de construire l'intervalle de confiance de la moyenne m.
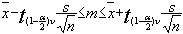
- Exemple
On a prélevé l'échantillon suivant
concernant des teneurs de principe actif (valeur en %)
40,39 - 42,93 - 4078 - 39,71 - 40,16 - 40,65 - 39,53 - 41,41
- 43,95 - 41,99
Déterminer l'intervalle de confiance de la moyenne m
( 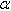 = 5%)
= 5%)
| n = 10 |
 = 41,15%
= 41,15% |
s = 1,4307% |
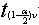 =2,262
pour =2,262
pour 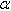 /2=2,5%
et pour /2=2,5%
et pour 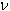 =9 =9 |
|
| D'où |
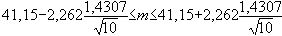 |
et |
 |
Graphique de la loi : cliquez
ici
|