L'intervalle de confiance d'une régression
Lorsqu'une
régression est validée quant à ses coefficients a et
b, on peut déterminer un intervalle
de confiance autour de cette droite.
Il
permet de connaître les limites de l'intervalle de confiance
de la régression pour certaines valeurs
de xo.
Dans le cadre de la détermination d'une date de péremption d'un produit périssable, c'est l'une des deux limites de cet intervalle qui permet de fixer cette échéance.
1
Préalables
2
Calculs
préalables
3
- Intervalle de prédiction
de la régression
4
- Application
5 - Extension de la prédiction
6
- Confusions possibles
La prévision d'une valeur est possible sous certaines conditions impératives.( aide mémoire pratique des techniques statistiques CERESTA)
- le nouvel individu doit être un élément de la population ayant fait l'objet de l'étude de régression à laquelle il se réfère,
- la valeur xo envisagée pour caractériser le nouvel individu considéré doit être comprise entre les valeurs extrêmes de la variable x utilisée lors de l'étude de la régression.
Il
en résulte qu'en toute rigueur on ne peut valablement effectuer
une prévision en dehors du cadre
des essais.
Toutefois,
il est possible d'effectuer de telles prévisions à titre
provisoire en attendant les résultats
des essais complémentaires.
| a | b |
| SCE1 = b |
SCEr = SCEt - SCE1 |
3 - Intervalle de prédiction de la régression
La prévision d'une valeur y se fait par la formule de la régression: y = a + b x0
| L'intervalle
bilatéral de prédiction au niveau (1 -
|
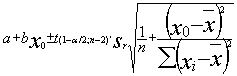 |
4
- Application
Soient
les valeurs de l'exemple fourni par le guide d'exploitation statistique
des résultats de stabilité
à long terme fourni en page 81 de STP Pharma pratiques 4 (2)
69-89 1994
Les
valeurs d'essais sont les suivantes:
| Lot 1 |
Lot 2 |
Lot 3 |
|||
| x
(mois) |
y
(%) |
x
(mois) |
y(%)
|
x
(mois) |
y(%) |
| 0 | 3,8 | 0 | 4,0 | 0 | 3,9 |
| 3 | 4,5 | 3 | 4,2 | 3 | 3,9 |
| 6 | 4,6 | 6 | 4,4 | 6 | 4,6 |
| 9 | 4,8 | 9 | 4,6 | 9 | 4,7 |
| 12 | 4,9 | 12 | 5,0 | 12 | 4,8 |
Ces valeurs correspondent à l'évolution de la teneur en impuretés d'une préparation pharmaceutique, concernant trois lots distincts, mesurée chaque trois mois. Une analyse préalable a permis de retenir une régression commune aux trois lots. Nous pouvons donc traiter les résultats comme s'ils provenaient du même lot.
| = 6 | = 4,4467 | ||
a |
= 3.9467 | b |
= 0,083333 |
| = 270 | = 2,177 | ||
SCE1 = b |
= 0,083333 x 0,083333 x 270 =1,875 | SCEr = SCEt - SCE1 |
= 2,177 - 1,875 = 0,302 |
| = 0,152 |
| L'intervalle de prédiction à 90 % (5 % de chaque côté) est alors obtenu par : |  |
On peut ainsi calculer toute valeur de y correspondant à une limite de l'intervalle de prédiction:
Exemple:
| pour
x = 0 y maxi = 4,07 y mini = 3,83 y moy = 3,95 |
pour
x = 12 y maxi = 5,07 y mini = 4,83 y moy = 4,95 |
Des
courbes caractérisant l'intervalle de prédiction peuvent
être tracées.
La
zone déterminée sur le graphique
correspond à la zone de prédiction des valeurs de la régression
dans l'intervalle de variation de x (0 à 12 mois)
5 - Extension de la prédiction
Nous proposons une extension de la zone de prédiction ainsi que le préconise le guide d'exploitation statistique des résultats de stabilité à long terme de la SFSTP afin de déterminer une estimation provisoire de la forme à péremption.
Cette estimation provisoire se doit être validée par la poursuite des essais en vue de confirmer ou d'infirmer les résultats.
Nous
venons de déterminer un intervalle de prédiction des valeurs
de la régression pour une valeur
quelconque de xo située dans le domaine étudié. Il
ne faut pas confondre cette zone de prédictions des valeurs de
la régression avec celle qui correspond
à la prédiction des valeurs individuelles de y ou encore
avec celle d'un intervalle de dispersion
constatée ne conduisant pas à une prédiction.
Nous
proposons de montrer les différences de résultats correspondant
à un exemple didactique
n=
10 ;
a=4 ; b=0,1; x=25
Domaine
étudié: x varie de 0 à 50
SCEX
=
![]() (xi-
(xi-![]() )
)![]() = 270
= 270
SCEr
=![]() (yi-(a+bxi))
(yi-(a+bxi))![]() =0,6
=0,6
S CE 1
= 0,1 x 0,1 x 270
= 2,7
t
= 6 (cette valeur importante a été choisie afin d'obtenir
des intervalles suffisamment
larges pour assurer la clarté des graphiques.
On
vérifie que la pente a une valeur significative au risque ![]() de 5 % par un test de Fisher.
de 5 % par un test de Fisher.
F = 2,7 / (0,6/8) = 36
La
pente a une valeur significative au risque ![]() de 5 % puisque la valeur du F correspondant (pour
de 5 % puisque la valeur du F correspondant (pour
![]() 1=
1 et
1=
1 et ![]() 2 = 8) est
de 5,32.
2 = 8) est
de 5,32.
La
détermination des intervalles est donc envisageable.
6 - 2 Intervalle de prédiction des valeurs individuelles y o ( graphique )
Les limites de l'intervalle sont déterminées à l'aide de la formule ci-dessous. Les valeurs correspondantes du chapitre 6 - 1 ont été utilisées.
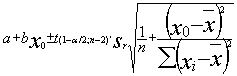
6 - 3 Zone de prédiction des y ( graphique )
Les limites de l'intervalle de la régression sont déterminées à l'aide de la formule ci-dessus.
Les valeurs correspondantes du chapitre 6 - 1 ont été utilisées.
Cet intervalle correspond à la zone de prédiction de la régression.
6 - 4 Zone de dispersion ( graphique )
Les
limites de l'intervalle sont déterminées à l'aide de
la formule ci-dessus.
Les valeurs correspondantes du chapitre 6 - 1 ont été utilisées.
C'est la zone contenant la majorité des individus de l'échantillon étudié.
Cet
intervalle ne permet pas la prédiction mais seulement l'analyse
des résultats (dispersion résiduelle
et tendance).