Test de Cochran
Le test de Cochran a pour objet la vérification de l'homogénéité des variances concernants plusieurs populations.
1. Conditions d'utilisation
2. Déroulement
3. Critère de décision
4. Tableau de calcul
5. Exemple d'application sur les teneurs en principes
actifs
6. Fiche
d'essai
7. Tableaux : valeurs critiques
de C
(n,k) : =0,05
; =0,01s
Plusieurs conditions sont nécessaires pour le pratiquer :
- les valeurs doivent être issus d'un tirage aléatoire effectué dans chacune des populations considérées,
- chaque échantillon doit être de taille identique,
- les distributions de la variable doivent obeir à des lois normales ou unimodales.
On prélève un échantillon de taille n dans chacune des k populations que l'on veut tester. On détermine :
la variance  pour
chaque échantillon : |
 |
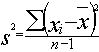| la plus grande des variances : | max |
| la somme des variances : |  |
| le rapport entre la plus grande des variances et la somme des variances : |  |
On lit la valeur de Ctable dans la table de
Cochran pour un risque
généralement choisi à 5% et pour n et k.
Ctable = C(n,k)
Si Ctest est plus petit ou gal à Ctable , alors on accepte l'hypothèse selon laquelle les variance des populations sont égales entre elles.
Dans le cas contraire, on rejette l'hypothèse d'égalité des variances.
Dans ce cas, on peut pratiquer un test de Dixon afin de détecter d'éventuelles valeurs aberrantes qui pourraient fausser les résultats.
| Groupe N°Valeur |
1 |
2 |
3 |
4 |
5 |
| 1 |
|||||
| 2 |
|||||
| 3 |
|||||
| 4 |
|||||
| 5 |
|||||
| 6 |
|||||
| 7 |
|||||
| = |
|||||
| = |
max= |
||||
| Ctest= | Ctable = C0.05(n,k) | ||||
| Décision : | |||||
5. Exemple d'application sur les teneurs en principes actifs
Il y a 5 sources de production. On vaut comparer les dispersions des 5 lots produits.
| Groupe N°Valeur |
A |
B |
C |
D |
E |
| 1 |
41,24 |
40,89 |
40,15 |
41,14 |
41,93 |
| 2 |
39,36 |
40,82 |
41,04 |
40,23 |
40,22 |
| 3 |
39,01 |
39,10 |
40,26 |
40,66 |
41,98 |
| 4 |
41,18 |
40,22 |
42,36 |
39,53 |
41,29 |
| 5 |
42,52 |
40,86 |
39,58 |
40,37 |
43,48 |
| 6 |
41,90 |
41,57 |
42,45 |
40,35 |
40,83 |
| 7 |
40,85 |
41,05 |
41,49 |
41,36 |
41,47 |
| = |
1,626 |
0,621 |
1,244 |
0,371 |
1,066 |
| =
4,928 |
max= 1,626 |
||||
| Ctest= 0,329 | Ctable = C0.05(n,k) = 0,478 | ||||
| Décision : pas de différence significative entre les variances des lots | |||||
