L'échantillonnage
L'échantillonnage consiste à prélever une fraction
limitée d'individus dans une population en vue d'obtenir des
informations sur cette population.
Ces informations peuvent servir de base à une décision
concernant la population ou le procédé qui l'a produite.
Si l'on veut que l'échantillon soit représentatif de
la population, on prélève un nombre suffisant d'individus
(n) dans la population (de taille N)
de telle sorte que tous les individus aient la même probabilité
d'être prélevés. (prélèvement au
hazard)
1. Domaine d'application.
2. Echantillonnage exhaustif _ non exhaustif.
3. Prélèvement au hazard.
4. Variables aléatoires discrètes - variables
aléatoires continues.
5. Echantillonnage - estimation ponctuelle.
6. Les lois d'échantillonnage.
7. Tableau de synthèse concernant l'échantillonnage.
- Chaque fois que l'analyse d'un phénomène ou d'une situation se fait à partir d'une fraction limitée de la population, ou des cas possibles, on peut parler d'échantillonnage.
- C'est le cas en contrôle de fabrication lorsque l'on veut surveiller un moyen de production, mais aussi en réception afin d'éviter d'avoir à contrôler tout le lot.
- Parfois le jugement sur échantillon est obligatoire si l'on ne veut pas détruire les individus (contrôles destructifs).
2. Echantillonnage exhaustif _ non exhaustif.
En statistique, on distingue les échantillonnages exhaustifs (qui épuisent) des autres qui sont dits non exaustifs.
Un échantillonnage est exhaustif à chaque fois que l'on prélève des individus sans les remettre dans le lot après examen. Pourtant, dans la pratique et pour des raisons de simplification, on considère qu'un prélèvement est non exhaustif si l'on prélève (sans remise) au plus 10% de la population du lot (exemple: un échantillon de 10 individus prélevé sans remise dans une population de 100 unités est considéré comme étant exhaustif)
Le plus souvent, ontraite donc les échantillons comme s'ils résultaient de prélévements non exhaustifs. C'est ce que nous ferons ci-après.
En principe, on devrait toujours prélever au hasard dans les
populations par exemple à l'aide table de "nombre au hasard".
En pratique, le respect strict du hasard serait beaucoup trop long
et trop coûteux.
Souvent, une bonne connaissance de la manière dont
est constitué le lot permet d'utiliser des arttifices satisfaisants.
Nous citerons, en particulier, la "stratification" dans les sondages d'opinion où, connaissant la répartition de la population par sexe, par profession, par lieu d'habitation et autres critères , on construit un échantillon correspondant à ces répartitions.
En production industrielle, on trouve le même phénomène pour des moyens de production différents, des heures ou des dates de fabrication, des tendances à dérive, etc... qui permettent d'utiliser des artifices adaptés.
Il va de soi qu'une bonne connaissance technique du produit permet toujours une meilleurs analyse du problème.
4. Variables aléatoires discrètes - variables aléatoires
continues.
En préalable à tout échantillonnage, il est nécessaire d'identifier la nature de la varaible qui régit la population.
On peut avoir à faire à des variables aléatoires discrètes ou à des variables aléatoires continues.
- Variables aléatoires continues
- une loi de distribution, par exemple une loi normale,
- un paramètre de position, par exemple la moyenne,
- un paramètre de dispersion, par exemple l'écart-type (voir loi normale)
- Varaibles aléatoires discrètes
Les variables aléatoires discrètes correspondent aux cas où l'identification des résultats se fait sous forme dichotomique.
Lorsque les valeurs de la variable peuvent être différentes et se situer sur une échelle continue, on parle de variables aléatoires continues.
Elles sont caractérisées par :
Exemple : 50% de la production est exportée en Allemagne.
0 0,5 1 Le segment bleu, égal à la moitié du segment total représente la fraction de la population exportée. Ce nombre (0,5) suffit pour caractériser cette variable discrète.
5. Echantillonnage - estimation ponctuelle.
En présence d'une population de caractéristique inconnue,
le problème est d'estimer cette caractéristique à
partir d'un échantillon de taille réduite.
Cet échantillon nous renseigne sur la caractéristique,
mais on ne peut affirmer que le résultat obtenu est le reflet
exact de la réalité. On peut estimer la réalité
par une estimation ponctuelle.
On prélève un échantillon de taille suffisante, ou une série d'échantillons. les caractéristiques de cet échantillonnage représentatif sont considérées comme étant celles de la population.
- Estimation d'une variable continue (loi normale)
Généralement, on choisit de prélever un échantillon
d'au moins 30 individus. La moyenne est estimée par 
qui se calcule comme la moyenne d'une population (m). L'écart-type
es testimé par la formule :
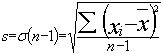nota : 
On remarque que le dénominateur est n (taille de l'échantillon)
dimiué d'une unité. On procéde ainsi pour obtenir
une estimation sans biais (correcte) et parce que dans le calcul de
s on a utilisé
qui est un estimateur de la moyenne m.
 |
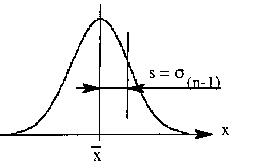Les valeurs de Exemple : On a prélevé
un échantillon de 50 individus dans un lot en respectant
les règles du hasard. on a calculé la moyenne
et l'écart-type de cet échantillon : Ces deux valeurs fournissent une estimation ponctuelle de la
moyenne m etde l'écart-type |
de
la population.- Estimation d'une variable discrète (proportion)
On prélève un échantillon de taille suffisante. 30 individus semblent être un minimum. On dénombre la proportion des individus ayant (ou n'ayant pas) la caractéristique recherchée. c'est ce nombre qui fourit l'estimation.
Exemple : On a prélevé un échantillon de 100 individus dans nu lot en respectant les régles du hasard. On a dénombré 3 individus défecteux. on peut calculer p = 3/100 = 0,03. Cette valeur fournit une estimation ponctuelle de la proportion de défecteux dans le lot.
6. Les lois d'échantillonnage.
Dans la majorité des cas, on se propose d'estimer la réalité (toujours inconnue) à l'aide d'échantillon de taille plus ou moins réduite.
Les lois d'échantillonnage permettent de construire des intervalles
de confiance ayant certaines chances de contenir la valeur vraie.
Des tests d'hypothèses variés permettent d'effectuer
des comparaisons et des validations. De nombreux essais de contrôle
exploitent ces lois d'échantillonnage.
De nombreuses lois sont disponibles. Nous nous limiterons à :
- la loi de Student et ses applications concernant les moyennes,
- la loi du khi_deux et ses applications concernant l'écart-type,
- la loi binomiale et ses applications concernant les proportions,
- la loi de Poisson et ses applications concernant les proportions dans le cas des faibles probabilités,
- la loi de Fisher et ses applications concernant les tests d'analyse de la variance,
Des approximations par des lois normales sont souvent ossibles. Elles sont valables à conditions que les échantillons soient de taille importante.
Nous ne les présentons pas ici car, dans la majorité des cas, les essais pharmaceutiques font appel à des échatillons de taille réduite.
7. Tableau de synthèse concernant l'échantillonnage.
Le tableau permet de mieux comprendre l'articulation des lois de population et des lois d'échantillonnage.
téléchargement : tableau.bmp(88ko) ou tableau.jpg(147ko)
